Уравнения, часть с

Задания с развернутым ответом: немного статистики

Многие думают, что эта часть ЕГЭ по математике очень сложная. Поэтому ребята, которые не рассчитывают на высокие баллы, даже не приступают к ней. И очень зря! С помощью этих заданий можно заработать дополнительные баллы и побороться за высокое место в рейтинге.

Сейчас будет немного статистики. В среднем около 30% учеников получают полные 2 балла за решение № 12, а вот неравенство № 14 дается хуже, только около 12% с ним справляются на полный балл. Геометрия даётся ещё хуже: стереометрию № 13 полностью решают 2% выпускников, планиметрию (№ 16) менее 5%. А вот с экономической задачей (№ 15) справляются около 15%, а это целых 2 балла! Что касается № 17 и 18, то они даются ещё хуже, но на то они и самые сложные, хотя 1 балл за № 18 по статистике получают около 25% сдающих — там нужно просто привести пример.

Какие темы важно знать для ЕГЭ по математике 2022?

В математике, как и в любом предмете, есть опорные темы. Если вы их выучите, будет легче справиться с экзаменом.

Формулы тригонометрии

Очень важно знать формулы тригонометрии и уметь применять их. Хорошая новость: в справочных материалах можно найти несколько тригонометрических формул

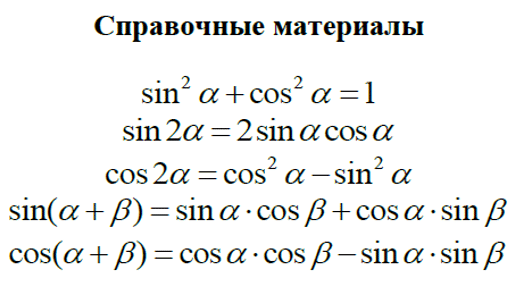
Но формул гораздо больше. Я советую не зубрить их, а научиться выводить: приходить к формулам шаг за шагом, опираясь на тождества. Кстати, мы учим выводить формулы на курсах подготовки к ЕГЭ: это полезно, чтобы оказаться на экзамене во всеоружии и ничего не перепутать.

Квадратные уравнения

Эти уравнения мы учимся решать еще в 7 классе. Они встречаются в ЕГЭ по математике постоянно: и как самостоятельные задания, и внутри более сложных уравнений или неравенств. Квадратные уравнения могут встретиться в математических моделях № 8 и № 15, в задачах на геометрию и стереометрию, в задании № 17 с параметром.

Самое главное — хорошо знать универсальные методы решения. Первый — через формулу дискриминанта, второй — через теорему Виета, которая может сэкономить время на экзамене.

Треугольники

Эта замечательная тема, которую проходят в 7 классе — основа основ всей геометрии. Она нужна и для решения стереометрии. и для простейших планиметрических задач. Еще треугольники необходимы, чтобы освоить огромное количество теорем

Выучите все, что с ними связано! Особое внимание обратите на прямоугольные треугольники, которые встречаются чаще остальных — тогда геометрические задачи сразу станут проще

Проценты

Самая нелюбимая тема моих учеников после тригонометрии, которую необходимо хорошо знать. Проценты нужны для реальной математики — это № 8 (с кратким ответом) и № 15 (с развернутым ответом). Понимание этой темы может принести вам 3 первичных балла.

Теория к заданию 4 из ЕГЭ по математике (профильной)

Вероятностью события $А$ называется отношение числа благоприятных для $А$ исходов к числу всех
равновозможных исходов

$P(A)={m}/{n}$, где $n$ – общее количество возможных исходов, а $m$ – количество исходов, благоприятствующих событию
$А$.

Вероятность события — это число из отрезка $$

В фирме такси в наличии $50$ легковых автомобилей. $35$ из них чёрные, остальные — жёлтые.
Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета.

Решение:

Найдем количество желтых автомобилей:

$50-35=15$

Всего имеется $50$ автомобилей, то есть на вызов приедет одна из пятидесяти. Желтых автомобилей $15$,
следовательно, вероятность приезда именно желтого автомобиля равна ${15}/{50}={3}/{10}=0,3$

Ответ:$0,3$

Противоположные события

Два события называются противоположными, если в данном испытании они несовместимы и одно из них обязательно
происходит. Вероятности противоположных событий в сумме дают 1.Событие, противоположное событию $А$, записывают
${(А)}{-}$.

$Р(А)+Р{(А)}{-}=1$

Независимые события

Два события $А$ и $В$ называются независимыми, если вероятность появления каждого из них не зависит от того,
появилось другое событие или нет. В противном случае события называются зависимыми.

Вероятность произведения двух независимых событий $A$ и $B$ равна произведению этих
вероятностей:

$Р(А·В)=Р(А)·Р(В)$

Иван Иванович купил два различных лотерейных билета. Вероятность того, что выиграет первый
лотерейный билет, равна $0,15$. Вероятность того, что выиграет второй лотерейный билет, равна $0,12$. Иван Иванович
участвует в обоих розыгрышах. Считая, что розыгрыши проводятся независимо друг от друга, найдите вероятность того,
что Иван Иванович выиграет в обоих розыгрышах.

Решения:

Вероятность $Р(А)$ — выиграет первый билет.

Вероятность $Р(В)$ — выиграет второй билет.

События $А$ и $В$ – это независимые события. То есть, чтобы найти вероятность того, что они произойдут оба
события, нужно найти произведение вероятностей

$Р(А·В)=Р(А)·Р(В)$

$Р=0,15·0,12=0,018$

Ответ: $0,018$

Несовместные события

Два события $А$ и $В$ называют несовместными, если отсутствуют исходы, благоприятствующие одновременно как событию
$А$, так и событию $В$. (События, которые не могут произойти одновременно)

Вероятность суммы двух несовместных событий $A$ и $B$ равна сумме вероятностей этих
событий:

$Р(А+В)=Р(А)+Р(В)$

На экзамене по алгебре школьнику достается один вопрос их всех экзаменационных. Вероятность
того, что это вопрос на тему «Квадратные уравнения», равна $0,3$. Вероятность того, что это вопрос на тему
«Иррациональные уравнения», равна $0,18$. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите
вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

Решение:

Данные события называются несовместные, так как школьнику достанется вопрос ЛИБО по теме «Квадратные уравнения»,
ЛИБО по теме «Иррациональные уравнения». Одновременно темы не могут попасться. Вероятность суммы двух
несовместных событий $A$ и $B$ равна сумме вероятностей этих событий:

$Р(А+В)=Р(А)+Р(В)$

$Р = 0,3+0,18=0,48$

Ответ: $0,48$

Совместные события

Два события называются совместными, если появление одного из них не исключает появление другого в одном и том же
испытании. В противном случае события называются несовместными.

Вероятность суммы двух совместных событий $A$ и $B$ равна сумме вероятностей этих событий минус
вероятность их произведения:

$Р(А+В)=Р(А)+Р(В)-Р(А·В)$

В холле кинотеатра два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится
кофе, равна $0,6$. Вероятность того, что кофе закончится в обоих автоматах, равна $0,32$. Найдите вероятность того,
что к концу дня кофе закончится хотя бы в одном из автоматов.

Решение:

Обозначим события, пусть:

$А$ = кофе закончится в первом автомате,

$В$ = кофе закончится во втором автомате.

Тогда,

$A·B =$ кофе закончится в обоих автоматах,

$A + B =$ кофе закончится хотя бы в одном автомате.

По условию, $P(A) = P(B) = 0,6; P(A·B) = 0,32$.

События $A$ и $B$ совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий,
уменьшенной на вероятность их произведения:

$P(A + B) = P(A) + P(B) − P(A·B) = 0,6 + 0,6 − 0,32 = 0,88$

Ответ: $0,88$

Самостоятельная подготовка к экзамену

К экзамену можно подготовиться самостоятельно с помощью методических пособий и интернет-источников. Мы составили список самого главного.

Методические пособия

Внимание: в некоторых пособиях осталась старая нумерация заданий: рекомендуются именно эти, так как новые ещё не выпустили

1. Ященко И. В. ЕГЭ-2022. ФИПИ. Математика. Типовые варианты экзаменационных заданий. 14 вариантов. Профильный уровень / И. В. Ященко . — М.: Экзамен, МЦНМО, 2022.
2. Ященко И. В. ЕГЭ-2022. ФИПИ. Математика. Типовые варианты экзаменационных заданий. 14 вариантов. Базовый уровень / И. В. Ященко . — М.: Экзамен, МЦНМО, 2022.
3. Вольфсон Г. И. ЕГЭ-2021. Математика. Арифметика и алгебра. Задача 19. Профильный уровень / Г. И. Вольфсон . — М.: МЦНМО, 2020.
4. Гордин Р. К. ЕГЭ-2021. Математика. Геометрия. Стереометрия. Задача 14. Профильный уровень. — М.: МЦНМО, 2021.
5. Гордин Р. К. ЕГЭ-2021. Математика. Решение задачи 16. Профильный уровень. — М.: МЦНМО, 2021.
6. Шестаков, С. А. ЕГЭ-2021. Задача с экономическим содержанием. Профильный уровень. — М.: МЦНМО, 2021.
7. Шестаков С. А. ЕГЭ-2021. Математика. Задачи с параметром. Задача 18. Профильный уровень. — М.: МЦНМО, 2021.
8. Шестаков С. А. ЕГЭ-2021. Математика. Неравенства и системы неравенств. Задача 15. Профильный уровень / С. А. Шестаков, П. И. Захаров. — М.: МЦНМО, 2021.
9. Шестаков С. А. ЕГЭ-2021. Математика. Уравнения и системы уравнений. Задача 13. Профильный уровень / С. А. Шестаков, П. И. Захаров. — М.: МЦНМО, 2021.

Интернет-источники

• «Рособрнадзор» — официальный ютьюб-канал Федеральной службы по надзору в сфере образования и науки, в котором публикуются видеоконсультации по подготовке к ЕГЭ.
• Теория по математике в Фоксфорд.Учебнике, раздел Математика, к некоторым темам прилагаются видео с объяснениями.
• Сайт Федерального института педагогических измерений — открытый банк заданий по всем предметам, демоверсии ЕГЭ и правила заполнения бланков в 2022 году.
• Утверждённые демоверсии ЕГЭ-2022 (базовый и профильный уровни).
• Сайт Бориса Трушина.

Ютьюб-каналы с разбором заданий

• Канал Бориса Трушина;
• «ЕГЭ Базовый уровень. Математика с нуля!»;
• «Школа Пифагора ЕГЭ по математике»;
• «Математик МГУ»;
• «Школково ЕГЭ, ОГЭ, олимпиады».

План подготовки к ЕГЭ по математике базового уровня

Когда в школе начинается подготовка к ЕГЭ по математике, базовый уровень экзамена часто игнорируют. Это может привести к досадным ошибкам. Чтобы их избежать, нужно разработать план подготовки.

Во-первых, стоит повторить основы, то есть математику 5-6 класса. Для этого можно использовать учебники, рекомендованные ФГОС, которые легко получить в школьной библиотеке или найти в интернете. От основ зависит успешная подготовка к ЕГЭ по математике: базовый уровень знаний обрести просто необходимо.

Во-вторых, прорешивайте задания каждого типа, не пропуская. Экзамен — всегда лотерея, поэтому никогда не предугадаешь, что тебе попадется. При решении некоторых заданий может оказаться бесполезна вся подготовка к ЕГЭ по математике: базовый уровень, несмотря на название, не предполагает, что все номера составлены без подводных камней.

В-третьих, не игнорируйте программу одиннадцатого класса. Структура экзамена редко совпадает с тем, что изучается в школе, но есть и исключения из правила. Когда начинается специализированная подготовка к ЕГЭ по математике, базовый уровень стереометрии, комбинаторики и некоторых других разделов, заложенный именно в одиннадцатом классе, позволяет успешно решать часть заданий КИМ.

Особенности уровней ЕГЭ по математике

В 2015 году ЕГЭ по математике разделили на базовый и профильный уровни. Это упростило жизнь выпускникам, которые не планируют поступать на специальности, связанные с математикой. Если ЕГЭ по математике нужен только для получения аттестата, можно сдать его облегченную версию, оставив время и силы для профильных экзаменов.

Базовый уровень ЕГЭ по математике

Как устроен базовый ЕГЭ по математике? Экзамен идет 180 минут, он состоит из 21 задания, за каждое из которых можно получить 1 балл. Этот экзамен единственный, который переводится не в 100-бальную систему, а в оценки.

Пока перевод баллов ЕГЭ по математике базового уровня в оценки не опубликован ФИПИ, но мы добавим его в статью, как только появится официальная информация.

В ЕГЭ по математике базового уровня 6 тематических блоков:

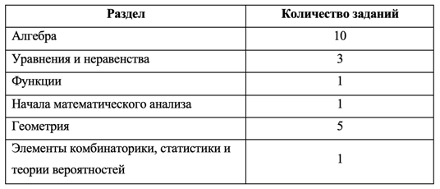
Тематические блоки, ЕГЭ по математике 2022, базовый уровень

Подробнее про базовый ЕГЭ по математике, включая разбор всех заданий, читайте здесь, а мы перейдём к профильному.

Профильный уровень ЕГЭ по математике

Данный экзамен, как и остальные ЕГЭ, переводится в 100-бальную систему.

Пока перевод баллов ЕГЭ по математике профильного уровня в 100-бальную систему пока не опубликован ФИПИ. Мы добавим его в статью, как только появится официальная информация.

Экзамен состоит из двух частей: Часть 1 с кратким ответом, а Часть 2 — с развернутым. Длится он 235 минут. Всего есть 18 заданий, которые разделены на 3 блока: алгебра, геометрия и реальная математика. Максимальное количество первичных баллов — 31.

База, профиль — неважно, к какому именно уровню вы готовитесь. В любом случае надо не только правильно решить каждое задание, но и оформить его так, чтобы проверяющие ни к чему не придрались

Нарисовать и описать график, расписать решение уравнения или задачи… И это не все: нужно еще и внести ответы в бланк без ошибок. И все это — за ограниченный период времени! Так можно перенервничать и запороть даже самую простую задачку. А на ЕГЭ — каждый балл на счету.Поэтому на своих занятиях я сразу показываю своим ученикам, как правильно оформлять каждое задание в ЕГЭ по математике. Мы разбираем все критерии и учимся правильно отвечать на вопросы. А еще я всегда помогаю ученикам закрыть пробелы в знаниях и объясняю сложные темы столько раз, сколько нужно. И куда же без лайфхаков? Всегда рассказываю лучший способ решения типичных заданий. Так что мои ученики приходят на экзамены подготовленными и не нервничают, когда видят задачу. Хотите также? Приходите ко мне на курсы подготовки к ЕГЭ по математике — научу!

Теория к заданию 12 из ЕГЭ по математике (профильной)

Наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение ординаты на рассматриваемом интервале.

Чтобы найти наибольшее или наименьшее значение функции необходимо:

1. Найти производную функции $f'(х)$
2. Найти стационарные точки, решив уравнение $f'(х)=0$
3. Проверить, какие стационарные точки входят в заданный отрезок.
4. Вычислить значение функции на концах отрезка и в стационарных точках из п.3
5. Выбрать из полученных результатов наибольшее или наименьшее значение.

Чтобы найти точки максимума или минимума необходимо:

1. Найти производную функции $f'(х)$
2. Найти стационарные точки, решив уравнение $f'(х)=0$
3. Разложить производную функции на множители.
4. Начертить координатную прямую, расставить на ней стационарные точки и определить знаки производной в полученных интервалах, пользуясь записью п.3.
5. Найти точки максимума или минимума по правилу: если в точке производная меняет знак с плюса на минус, то это будет точка максимума (если с минуса на плюс, то это будет точка минимума). На практике удобно использовать изображение стрелок на промежутках: на промежутке, где производная положительна, стрелка рисуется вверх и наоборот.

Таблица производных некоторых элементарных функций:

Функция	Производная
$c$	$0$
$x$	$1$
$x^n, n∈N$	$nx^{n-1}, n∈N$
${1}/{x}$	$-{1}/{x^2}$
${1}/x{^n}, n∈N$	$-{n}/{x^{n+1}}, n∈N$
$√^n{x}, n∈N$	${1}/{n√^n{x^{n-1}}, n∈N$
$sinx$	$cosx$
$cosx$	$-sinx$
$tgx$	${1}/{cos^2x}$
$ctgx$	$-{1}/{sin^2x}$
$cos^2x$	$-sin2x$
$sin^2x$	$sin2x$
$e^x$	$e^x$
$a^x$	$a^xlna$
$lnx$	${1}/{x}$
$log_{a}x$	${1}/{xlna}$

Основные правила дифференцирования

1. Производная суммы и разности равна производной каждого слагаемого

$(f(x) ± g(x))′= f′(x)± g′(x)$

Пример:

Найти производную функции $f(x) = 3x^5 – cosx + {1}/{x}$

Производная суммы и разности равна производной каждого слагаемого

$f′(x)=(3x^5)′–(cosx)′+({1}/{x})’=15x^4+sinx-{1}/{x^2}$

2. Производная произведения.

$(f(x)∙g(x))′=f′(x)∙g(x)+f(x)∙g(x)′$

Пример:

Найти производную $f(x)=4x∙cosx$

$f′(x)=(4x)′∙cosx+4x∙(cosx)′=4∙cosx-4x∙sinx$

3. Производная частного

$({f(x)}/{g(x)})’={f^'(x)∙g(x)-f(x)∙g(x)’}/{g^2(x)}$

Пример:

Найти производную $f(x)={5x^5}/{e^x}$

$f'(x)={(5x^5)’∙e^x-5x^5∙(e^x)’}/{(e^x)^2}={25x^4∙e^x-5x^5∙e^x}/{(e^x)^2}$

4. Производная сложной функции равна произведению производной внешней функции на производную внутренней функции

$f(g(x))′=f′(g(x))∙g′(x)$

Пример:

$f(x)= cos(5x)$

$f′(x)=cos′(5x)∙(5x)′= — sin(5x)∙5= -5sin(5x)$

Пример:

Найдите точку минимума функции $y=2x-ln⁡(x+11)+4$

Решение:

1. Найдем ОДЗ функции: $х+11>0; х>-11$

2. Найдем производную функции $y’=2-{1}/{x+11}={2x+22-1}/{x+11}={2x+21}/{x+11}$

3. Найдем стационарные точки, приравняв производную к нулю

${2x+21}/{x+11}=0$

Дробь равна нулю если числитель равен нулю, а знаменатель не равен нулю

$2x+21=0; x≠-11$

$2х=-21$

$х=-10,5$

4. Начертим координатную прямую, расставим на ней стационарные точки и определим знаки производной в полученных интервалах. Для этого подставим в производную любое число из крайней правой области, например, нуль.

$y'(0)={2∙0+21}/{0+11}={21}/{11}>0$

5. В точке минимума производная меняет знак с минуса на плюс, следовательно, точка $-10,5$ — это точка минимума.

Ответ: $-10,5$

Пример:

Найдите наибольшее значение функции $y=6x^5-90x^3-5$ на отрезке $$

Решение:

1. Найдем производную функции $y′=30x^4-270x^2$

2. Приравняем производную к нулю и найдем стационарные точки

$30x^4-270x^2=0$

Вынесем общий множитель $30x^2$ за скобки

$30x^2(x^2-9)=0$

$30x^2(х-3)(х+3)=0$

Приравняем каждый множитель к нулю

$x^2=0 ; х-3=0; х+3=0$

$х=0;х=3;х=-3$

3. Выберем стационарные точки, которые принадлежат заданному отрезку $$

Нам подходят стационарные точки $х=0$ и $х=-3$

4. Вычислим значение функции на концах отрезка и в стационарных точках из п.3

$y(-5)= 6∙(-5)^5-90∙(-5)^3-5=6∙(-3125)+90∙125-5= -18750+11250-5=-7505$

$y(-3)= 6∙(-3)^5-90∙(-3)^3-5=-1458+2430-5=967$

$y(0)= -5$

$y(1)= 6∙1^5-90∙1^3-5=6-90-5= -89$

Наибольшее значение равно $967$

Ответ: $967$

Дробно рациональные уравнения

• Если дробь равна нулю, то числитель равен нулю, а знаменатель не равен нулю.
• Если хотя бы в одной части рационального уравнения содержится дробь, то уравнение называется дробно-рациональным.

Чтобы решить дробно рациональное уравнение, необходимо:

1. Найти значения переменной, при которых уравнение не имеет смысл (ОДЗ)
2. Найти общий знаменатель дробей, входящих в уравнение;
3. Умножить обе части уравнения на общий знаменатель;
4. Решить получившееся целое уравнение;
5. Исключить из его корней те, которые не удовлетворяют условию ОДЗ.

Если в уравнении участвуют две дроби и числители их равные выражения, то знаменатели можно приравнять друг к другу и решить полученное уравнение, не обращая внимание на числители. НО учитывая ОДЗ всего первоначального уравнения

Показательные уравнения

Показательными называют такие уравнения, в которых неизвестное содержится в показателе степени.

$a^x=b$

При решении показательных уравнений используются свойства степеней, вспомним некоторые из них:

1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются.

$a^n·a^m=a^{n+m}$

2. При делении степеней с одинаковыми основаниями основание остается прежним, а показатели вычитаются

$a^n:a^m=a^{n-m}$

3. При возведении степени в степень основание остается прежним, а показатели перемножаются

$(a^n)^m=a^{n∙m}$

4. При возведении в степень произведения в эту степень возводится каждый множитель

$(a·b)^n=a^n·b^n$

5. При возведении в степень дроби в эту степень возводиться числитель и знаменатель

$({a}/{b})^n={a^n}/{b^n}$

6. При возведении любого основания в нулевой показатель степени результат равен единице

$a^0=1$

7. Основание в любом отрицательном показателе степени можно представить в виде основания в таком же положительном показателе степени, изменив положение основания относительно черты дроби

$a^{-n}={1}/{a^n}$

${a^{-n}}/{b^{-k}}={b^k}/{a^n}$

8. Радикал (корень) можно представить в виде степени с дробным показателем

$√^n{a^k}=a^{{k}/{n}}$

Виды показательных уравнений:

1. Простые показательные уравнения:

а) Вида $a^{f(x)}=a^{g(x)}$, где $а >0, a≠1, x$ — неизвестное. Для решения таких уравнений воспользуемся свойством степеней: степени с одинаковым основанием ($а >0, a≠1$) равны только тогда, когда равны их показатели.

$f(x)=g(x)$

b) Уравнение вида $a^{f(x)}=b, b>0$

Для решения таких уравнений надо обе части прологарифмировать по основанию $a$, получается

$log_{a}a^{f(x)}=log_{a}b$

$f(x)=log_{a}b$

2. Метод уравнивания оснований.

3. Метод разложения на множители и замены переменной.

• Для данного метода во всем уравнении по свойству степеней надо преобразовать степени к одному виду $a^{f(x)}$.
• Сделать замену переменной $a^{f(x)}=t, t > 0$.
• Получаем рациональное уравнение, которое необходимо решить путем разложения на множители выражения.
• Делаем обратные замену с учетом того, что $t > 0$. Получаем простейшее показательное уравнение $a^{f(x)}=t$, решаем его и результат записываем в ответ.

Пример:

Решите уравнение $2^{3x}-7·2^{2x-1}+7·2^{x-1}-1=0$

Решение:

По свойству степеней преобразуем выражение так, чтобы получилась степень 2^x.

$(2^x)^3-{7·(2^x)^2}/{2}+{7·2^x}/{2-1}=0$

Сделаем замену переменной $2^x=t; t>0$

Получаем кубическое уравнение вида

$t^3-{7·t^2}/{2}+{7·t}/{2}-1=0$

Умножим все уравнение на $2$, чтобы избавиться от знаменателей

$2t^3-7·t^2+7·t-2=0$

Разложим левую часть уравнения методом группировки

$(2t^3-2)-(7·t^2-7·t)=0$

Вынесем из первой скобки общий множитель $2$, из второй $7t$

$2(t^3-1)-7t(t-1)=0$

Дополнительно в первой скобке видим формулу разность кубов

$2(t-1)(t^2+t+1)-7t(t-1)=0$

Далее скобку $(t-1)$ как общий множитель вынесем вперед

$(t-1)(2t^2+2t+2-7t)=0$

Произведение равно нулю, когда хотя бы один из множителей равен нулю

1) $(t-1)=0;$ 2) $2t^2+2t+2-7t=0$

Решим первое уравнение

$t_1=1$

Решим второе уравнение через дискриминант

$2t^2-5t+2=0$

$D=25-4·2·2=9=3^2$

$t_2={5-3}/{4}={1}/{2}$

$t_3={5+3}/{4}=2$

Получили три корня, далее делаем обратную замену и получаем три простых показательных уравнения

$2^x=1; 2^x={1}/{2}; 2^x=2$

$2^x=2^0; 2^x=2^{-1}; 2^x=2^1$

$х_1=0; х_2=-1; х_3=1$

Ответ: $-1; 0; 1$

4. Метод преобразования в квадратное уравнение

• Имеем уравнение вида $А·a^{2f(x)}+В·a^{f(x)}+С=0$, где $А, В$ и $С$ — коэффициенты.
• Делаем замену $a^{f(x)}=t, t > 0$.
• Получается квадратное уравнение вида $A·t^2+B·t+С=0$. Решаем полученное уравнение.
• Делаем обратную замену с учетом того, что $t > 0$. Получаем простейшее показательное уравнение $a^{f(x)}=t$, решаем его и результат записываем в ответ.

Способы разложения на множители:

Вынесение общего множителя за скобки.

Чтобы разложить многочлен на множители путем вынесения за скобки общего множителя надо:

1. Определить общий множитель.
2. Разделить на него данный многочлен.
3. Записать произведение общего множителя и полученного частного (заключив это частное в скобки).

Пример:

Разложить на множители многочлен: $10a^{3}b-8a^{2}b^2+2a$.

Общий множитель у данного многочлена $2а$, так как на $2$ и на «а» делятся все члены. Далее найдем частное от деления исходного многочлена на «2а», получаем:

$10a^{3}b-8a^{2}b^2+2а=2a({10a^{3}b}/{2a}-{8a^{2}b^2}/{2a}+{2a}/{2a})=2a(5a^{2}b-4ab^2+1)$

Это и есть конечный результат разложения на множители.

Разбор заданий ЕГЭ по базовой математике

Когда в школах начинается подготовка к ЕГЭ по математике, базовый уровень предмета просто нарешивают, не пытаясь разобрать задания. Чтобы разобраться в решении номеров, следует помнить основные типы встречающихся задач:

Текстовые задачи — сюда входят задачи на проценты, округление и смелкалку. Задачи на проценты решаются через умножение (процент принимается за десятичную дробь — 15% = 0,15). Задачи на округление решаются через деление с помощью логики. Задача №20 решается методом подбора.
Вычисления и преобразования — блок заданий, проверяющих умение обращаться с дробями и степенями, а также с тригонометрическими и иррациональными выражениями. Предполагается, что когда начинается подготовка к ЕГЭ по математике, базовый уровень знаний и умение обращаться с формулами, данными в начале КИМ, у вас уже имеется

В заданиях важно уметь подставлять необходимые значения в формулы и производить вычисления по этим формулам, а также записывать числа в разных видах.
Размеры и единицы измерения — чтобы решить задания этого раздела, необходимо знать порядок возрастания величин времени, длины, массы, объема, площади и уметь сопоставлять их с реальными объектами.
Фигуры — для решения заданий данного блока нужно знать основные понятия (единицы измерения и части фигур), а также уметь сопоставлять их с реальными фигурами и использовать эти данные при решении задач. Например, когда идет подготовка к ЕГЭ по математике, базовый уровень владения стереометрией должен позволять определить объем фигур, площадь их боковых граней и тому подобное.
Анализ информации — на экзамене информация представлена в виде графиков, диаграмм и текста

Для решения заданий нужно пронаблюдать за изменениями величин, а также найти наибольшую из них. Проверяется умение анализировать информацию или выбирать оптимальный вариант, опираясь на логическое мышление.
Уравнения и неравенства — проверяется умение использовать данные формулы, выводить из них другие, а также отмечать значения на числовой прямой. Все это обеспечит хорошая подготовка к ЕГЭ по математике: базовый уровень заданий раздела предполагает, что они с большей вероятностью будут типовыми и без подводных камней, к которым привыкают выпускники, сдающие профиль, и учителя.
Теория вероятностей (1 задание) — задание, решающееся с помощью определения нужной формулы комбинаторики (их всего три) и подставления в нее значений из задачи.

Физический смысл производной

Если материальная точка движется прямолинейно и ее координата изменяется в зависимости от времени по закону $x(t)$, то мгновенная скорость данной точки равна производной функции.

$v(t) = x'(t)$

Точка движется по координатной прямой согласно закону $x(t)= 1,5t^2-3t + 7$, где $x(t)$ — координата в момент времени $t$. В какой момент времени скорость точки будет равна $12$?

Решение:

1. Скорость – это производная от $x(t)$, поэтому найдем производную заданной функции

$v(t) = x'(t) = 1,5·2t -3 = 3t -3$

2. Чтобы найти, в какой момент времени $t$ скорость была равна $12$, составим и решим уравнение:

$3t-3 = 12$

$3t = 15$

$t = 5$

Ответ: $5$

Метод группировки

Методом группировки удобно пользоваться, когда на множители необходимо разложить многочлен с четным количеством слагаемых. В данном способе необходимо собрать слагаемые по группам и вынести из каждой группы общий множитель за скобку. У нескольких групп после вынесения в скобках должны получиться одинаковые выражения, далее эту скобку как общий множитель выносим вперед и умножаем на скобку полученного частного.

Пример:

Разложить многочлен на множители $2a^3-a^2+4a-2$

Решение:

Для разложения данного многочлена применим метод группировки слагаемых, для этого сгруппируем первые два и последние два слагаемых, при этом важно правильно поставить знак перед второй группировкой, мы поставим знак + и поэтому в скобках запишем слагаемые со своими знаками. $2a^3-a^2+4a-2=(2a^3-a^2)+(4a-2)$

$2a^3-a^2+4a-2=(2a^3-a^2)+(4a-2)$

Далее из каждой группы вынесем общий множитель

$(2a^3-a^2)+(4a-2)=a^2(2a-1)+2(2a-1)$

После вынесения общих множителей получили пару одинаковых скобок. Теперь данную скобку выносим как общий множитель.

$a^2(2a-1)+2(2a-1)=(2a-1)(a^2+2)$

Произведение данных скобок — это конечный результат разложения на множители.